前言
本文主要是学习BP神经网络的一个总结,其本身也是机器学习中比较基础、适合入门的模型。 目前本人对于机器学习也还只是入门状态,对于很多名词仍然是一知半解(感觉机器学习中的很多术语本身也是模棱两可的),对于很多公式也是不求甚解,因此这篇文章是尝试用自己的语言和理解来复述所学习到的知识,如果有错误之处还望大牛们不吝斧正。
霍金说过每多一个数学公式,就会少一半的读者,因此这里也会尽量少用公式,要用也只用简单易懂的公式。而且个人觉得神经网络中的很多公式是可以感性地去认识的,能完全明白推导过程自然最好,但在不求甚解的状态下能达到感性的认知也未必不是一个快速掌握的好方法。
另外本文中用到了不少矩阵相关的知识,忘记了的同学可以看附录中的整理。
神经元与激励函数
神经元
神经元是神经网络的基本组成,如果把它画出来,大概就长成下面这样:
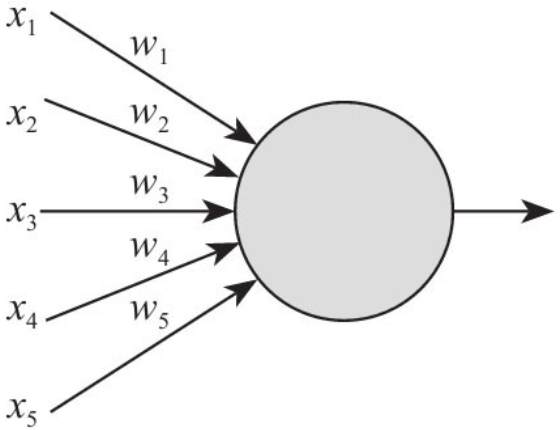
图中神经元左边的x表示对神经元的多个输入,w表示每个输入对应的权重,神经元右边的箭头表示它仅有一个输出。
当然神经元也有很多种,下面介绍两种比较基础的。
神经元1:感知器
神经网络技术起源于上世纪五、六十年代,当时叫感知机(perceptron),其中的单个神经元我们可以叫作感知器。感知器的特点具有浓厚的时代气息:其输入输出都是二进制形式的(据说由于计算技术的落后,当时感知器传输函数是用线拉动变阻器改变电阻的方法机械实现的)。
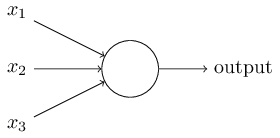
如上图所示,感知器有多个二进制输入(值只能是0或1) \(X_{1}\)、\(X_{2}\)..\(X_{n}\),每个输入有对应的权值\(W_{1}\)、\(W_{2}\)..\(W_{n}\)(图中没画出来),将每个输入值乘以对应的权值再求和(\(\sum_j X_{j} W_{j}\)),然后与一个阈值(threshold) 比较,大于阈值则输出1、小于阈值则输出0。 写成公式的话如下:
\[ output = \begin{cases} 0 &\text{if } \sum_j w_j x_j \leq threshold \\ 1 &\text{if } \sum_j w_j x_j > threshold \end{cases} \]
如果把公式写成矩阵形式,再用b来表示负数的阈值(即b=-threshold),那就得到了如下公式:
\[ output = f(x) = \begin{cases} 0 &\text{if } w x + b \leq 0 \\ 1 &\text{if } w x + b > 0 \end{cases} \]
举个栗子
例如你所在的城市将有一个你的偶像的演唱会,你正决定是否观看,你可能会通过以下三个方面来权衡你的决定:
- 天气好吗?
- 你的好基友是否愿意陪你去?
- 是否这个活动距离公共交通很近?(你自己没车)
我们将这三个因素用对应的二进制变量\(x_1\),\(x_2\)和\(x_3\)表示。比如,当天气还不错时,我们有\(x_1\)=1,天气不好时\(x_1\)=0;相似的,如果好基友愿意去,\(x_2\)=1,否则\(x_2\)=0;对于公共交通\(x_3\)同理赋值。
然后根据你的意愿,比如让天气权重 \(w_1\)=6,其他条件权重分别为\(w_2\)=2,\(w_3\)=2。权重\(w_1\)值越大表示天气影响最大,比起好基友加入或者交通距离的影响都大。最后,假设你选择5做为感知器阈值(即b为-5),按照这种选择,这个感知器就能实现这个决策模型:当天气好时候输出1,天气不好时候输出0,无论你的好基友是否愿意去,或者交通是否比较近。
神经元2:Sigmoid神经元
先来认识一个函数:Sigmoid函数,这个单词在某些工具上直译是“乙状结肠”、也还真有某些资料把Sigmoid神经元叫作乙状结肠神经元的。 其实它是一个常用的“S”型函数,可以把变量映射到(0,1)区间内,其公式如下:
\[ \sigma (z) = \dfrac{1}{1+e^{-z}} \]
它的函数图像是如下图如示的“S”型:
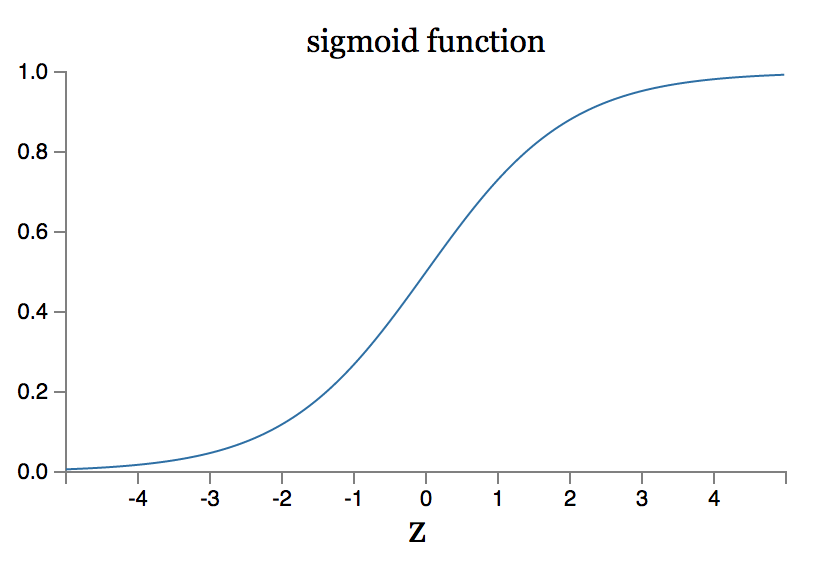
那么Sigmoid神经元是什么呢?与感知器有什么区别?
首先,在Sigmoid神经元中,输入的值不再是二进制,而是0到1之间的任意值。即\(X_i\)取值是0到1之间的任意实数。
其次,而Sigmoid神经元的输出也不再是0或1,而是 σ(wx+b)。 注意"wx+b"是简写(矩阵)形式,请对照上面的感知器的公式。
因此我们可以得出Sigmoid神经元的公式:
\[ output = f(x) = \dfrac{1}{1+e^{-(wx+b)}} \]
可以发现当z=w⋅x+b是一个大的正数时,那么σ(z)≈1,而当z=w⋅x+b是一个很小的负数(“绝对值很大的负数”比较好理解)时,σ(z)≈0。处于这两种情况时,Sigmoid神经元的输出跟感知器是很接近的。只有当w⋅x+b在一个适度的值,sigmoid神经元和感知器偏差才较大。
激励函数
神经元的输入和输出之间具有函数关系,这个函数就称为激励函数。所以上面提到的Sigmoid函数就是激励函数的一种,感知器的那个函数也可以称为阈值(或阶跃)激励函数。
激励函数也叫点火规则,这使它与人脑的工作联系起来。当一个神经元的输入足够大时,就会点火,也就是从它的轴突(输出连接)发送电信号。同样,在人工神经网络中,只要输入超过一定标准时才会产生输出,这就是点火规则的思想。
神经网络的结构
神经网络简单地说就是将多个神经元连接起来、组成一个网络。 本文介绍的是最简单、历史悠久的一种:“多层感知机”(但我们讲的这个它里面的神经元并不是感知器、而是Sigmoid神经元,名词混乱+1),或称之为“多层向前神经网络(Multilayer Feed-Forward Neural Network)”,它的特点是有多层(废话),且神经元之间是全连接的,即后一层的神经元会连接到前一层的每个神经元(这里定义下从输入层到输出层为从“后”向“前”)。
一个多层感知机的示意图如下,网络的最左边一层被称为输入层,其中的神经元被称为输入神经元。最右边及输出层包含输出神经元,在这个例子中,只有一个单一的输出神经元,但一般情况下输出层也会有多个神经元。中间层被称为隐含层,因为里面的神经元既不是输入也不是输出。
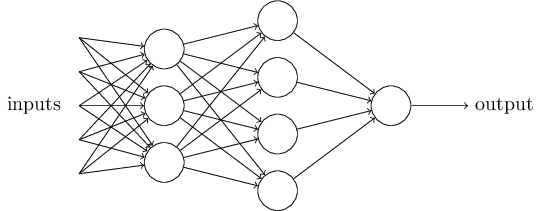
训练神经网络的意义
现在神经元有了,神经网络的结构也有了,现在回到核心的问题上来:我们拿神经网络干什么? 要怎样使它做到?
训练的目标
按照常识、用人话来说,神经网络的作用就是我们预先给它大量的数据(包含输入和输出)来进行训练,训练完成后,我们希望它对于将来的真实环境的输入也能给出一个令我们满意的输出。
损失函数/代价函数(Loss函数)
那么怎样用数学的方式来表示一个输出有多么令我们满意呢? 这里我们引入损失函数(或称代价函数、Loss函数)的概念。
现假设有n组包含了输入和真实结果(或称期望结果、期望输出)的样本数据,对于每组输入,我们的神经网络输出的结果记为fi,真实结果(期望结果)记为yi。
使用数学工具中的MAE(Mean Absolute Error,平均绝对误差),可以非常直观地表达出输出结果和真实结果的偏差,因此我们可以用MAE来写出一个下面这样的Loss函数,Loss值越大、说明神经网络的输出结果越远离我们的期望。
\[ Loss = \dfrac{1}{n} \sum_{i=1}^n \vert f_i - y_i \vert \]
也可以用MSE(Mean Squared Error,均方误差)作为损失函数,MSE能更好地评价数据的变化程度,简单地说因为平方了一下、偏差是会被放大的。
\[ Loss = \dfrac{1}{n} \sum_{i=1}^n (f_i - y_i)^2 \]
将Sigmoid神经元的表达式f(x)=σ(wx+b)代入上面的损失函数中,可以发现x(输入)是固定的,\(y_i\)(期望结果)也是固定的,让我们感性地想象一下:实际上影响Loss的只有w和b,而最重要的任务也就是寻找w和b使得Loss最小。
再具象一点,其实对神经网络进行训练的目的就是为每个神经元找到最适合它的w和b的值,从而使得整个神经网络的输出最接近我们的期望(说“最”其实有点违反广告法,神经网络最终达到的很难说是问题的最优解)。
注:下面将真正用到的损失函数
在实际中,为了方便求导,一般使用如下的Loss函数:
\[ Loss = \dfrac{1}{2n} \sum_{i=1}^n (f_i - y_i)^2 \]
梯度下降
根据上面的结论,可以把损失(Loss)记作C,而C又只与w和b有关,那么可以看成C是一个关于w和b的函数,如下图所示。注意由于神经网络中其实有大量的“w”和“b”(回忆一下、每个神经元都有多个权重和一个阈值),因此这里也需要感性的认知。
\[ C = f(w,b) \]
如果把图画出来,它可能是下面这样的:

我们的目标是找到w和b使C最小,当然上面这张图很容易看出来合适的w和b在哪,但当面对更复杂的情况时、比如下图这样的,应该如何快速地找到C最小的点呢?
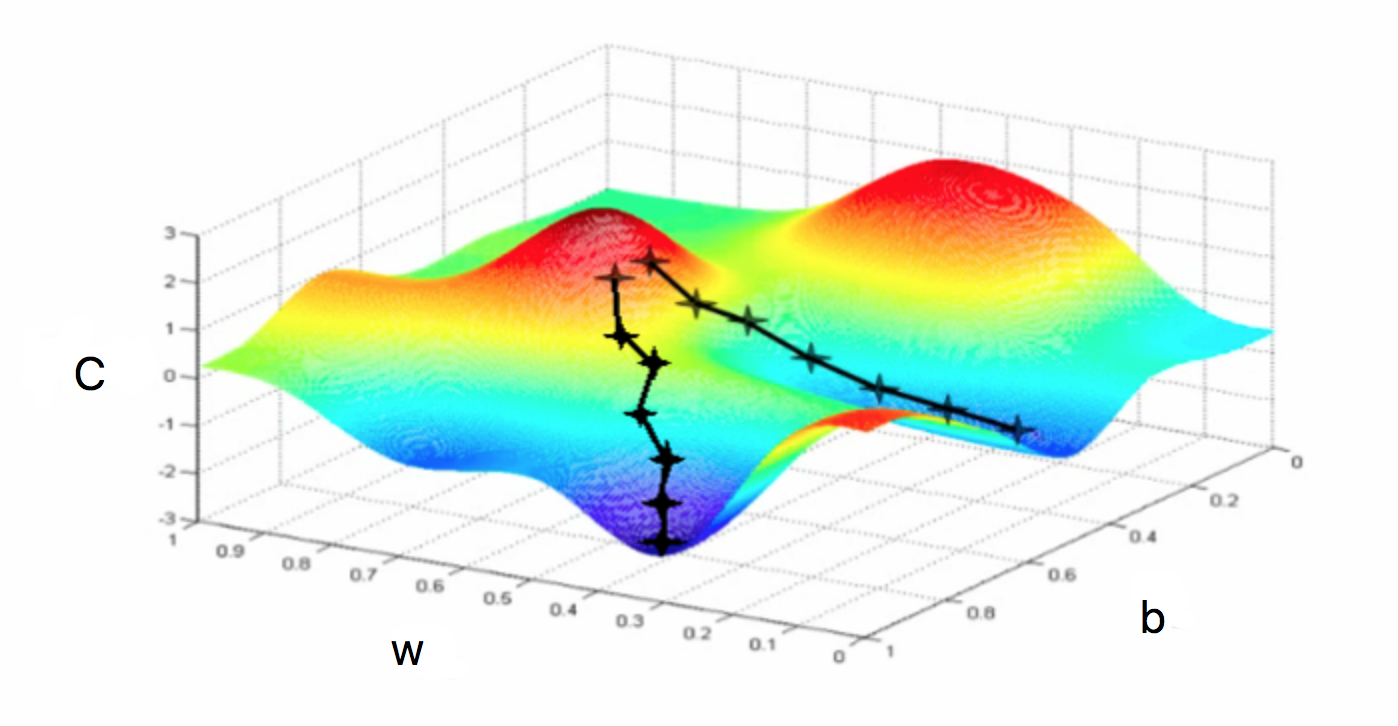
这里我们引入梯度下降算法,原理很简单:把上图看作是一个丘陵地带,想象我们有一个球放在某个位置,让它“自然地向低处滚”,滚得越低,C就越小,我们就越高兴。
那么怎样使得它往低处滚呢? (注意这里要搬出全文中第一个比较烧脑的概念了) 微分法则告诉我们,当w移动Δw、b移动Δb时,有:
\[ \Delta C \approx \dfrac{ \partial C}{\partial w} \Delta w + \dfrac{ \partial C}{\partial b} \Delta b \]
由于C表示的是损失,我们想让球往低处滚,当然是希望C不断变小,那ΔC应该恒为负,那么Δw、Δb应该如何取值呢? 梯度下降法是这么设计的:
\[ \Delta w = - \eta \dfrac{ \partial C}{\partial w} \qquad \Delta b = - \eta \dfrac{ \partial C}{\partial b} \]
可以看出如此取值可以使ΔC恒为负,其中的η称为**学习率。
那么现在问题变成了∂C/∂w、∂C/∂b,即 C对w 和 C对b 的偏导,这两个鬼东西要怎么求
反向传播
反向传播(back propagation)是在这种场景下快速求解∂C/∂w、∂C/∂b的算法,用了这个算法的多层感知机--也就是这篇文章讲的神经网络--也就叫作BP神经网络(名词混乱+1)。
这一章包含了比较复杂的公式推导过程,个人认为不了解其细节也没有关系、可以跳过这一章(只看“正向传播”一节就行),只要知道有个经典的反向传播算法可以快速求解∂C/∂w、∂C/∂b,从而算出Δw和Δb,使得ΔC恒为负、即使得Loss越来越小即可。
正向传播
正向传播也可以叫作前馈(所以又有个前馈神经网络的词...),正向传播就是指给神经网络的输入,然后一层一层向前计算输出,最终得到一个输出,这就是正向传播了。
推导前的基本定义
w、a、b的定义
我们使用 \(w^l_{jk}\) 表示从 \((l−1)_{th}\) 层的 \(k_{th}\) 个神经元到 \((l)_{th}\) 层的 \(j_{th}\) 个神经元的链接上的权重。例如,下图给出了第二隐藏层的第四个神经元到第三隐藏层的第二个神经元的链接上的权重:
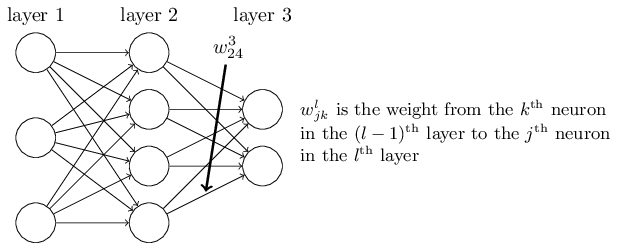
我们使用 \(b^l_j\) 表示在 \(l_{th}\) 层 \(j_{th}\) 个神经元的偏差,使用 \(a^l_j\) 表示 \(l_{th}\) 层 \(j_{th}\) 个神经元的激活值。下面的图清楚地解释了这样表示的含义:
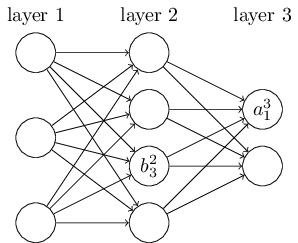
基于上面的定义,可以写出关于单个神经元激活值alj的公式,其中sum(l-1)表示(l−1)th 层的神经元数量:
\[ a^{l}_{j} = \sigma ( \sum_{k=1}^{sum(l-1)} w^{l}_{jk} a^{l-1}_{k} + b^{l}_{j}) \]
上面w的表示方法或许很奇怪,但我们把它写成矩阵形式或许就能发现它的妙处了。用\(w^l\)矩阵来表示第(l)th 层的w的值,用j作为行,k行为列,那么上面的神经网络中的w3就可以写成:
\[ w^3 = \begin{bmatrix} w^3_{1 1} & w^3_{1 2} & w^3_{1 3} & w^3_{1 4} \\ w^3_{2 1} & w^3_{2 2} & w^3_{2 3} & w^3_{2 4} \end{bmatrix} \]
那么也可以用\(a^l\)矩阵来表示第(l)th 层的a的值,用j作为行,但只有一列,那么\(a^l\)其实是一个列向量。那么上面的a2可以写成下面非常形象的列向量形式:
\[ a^2 = \begin{bmatrix} a^2_1 \\ a^2_2 \\ a^2_3 \\ a^2_4 \end{bmatrix} \]
同理,b3可以也可以写成一个列向量:
\[ b^3 = \begin{bmatrix} b^3_1 \\ b^3_2 \end{bmatrix} \]
那么由上面的单个神经元激活值\(a^l_j\)的公式,可以得出\(a^l\)矩阵的公式:
\[ a^l = \sigma (w^l a^{l-1} + b^l) \]
单个神经元的带权输入\(z^l_j\)
从上面的公式中可以提取出一个中间量\(z^l_j\):
\[ z^{l}_{j} = \sum_{k=1}^{sum(l-1)} w^{l}_{jk} a^{l-1}_{k} + b^{l}_{j} \qquad a^{l}_{j} = \sigma (z^{l}_{j}) \]
当然也可以简写成矩阵形式:
\[ z^l = w^l a^{l-1} + b^l \qquad a^l = \sigma (z^{l}) \]
\(z^l_j\)其实就是第 l 层第 j 个神经元的激活函数带权输入。
单组数据的损失
前面介绍了损失函数,那么对于某一组输入,其损失(大写的“L”表示输出层)可以写作如下公式(这里比上面的Loss公式少了个n,因为这里只考虑一组输入,而上面的Loss设定是考虑n组数据)。
\[ C = \dfrac{1}{2} \sum_{j=1}^{sum(L)} (a^L_j - y_j)^2 \]
这个公式同样可以写成矩阵的形式,这里用到了矩阵的模(可以看附录),模的平方即为向量各元素的平方和。
\[ C = \dfrac{1}{2} \lVert a^L - y \rVert ^2 \]
单个神经元的误差\(δ^l_j\)测试
定义 l 层的第 \(j_{th}\) 个神经元上的误差 \(δ^l_j\) 为:
\[ \delta^{l}_{j} = \dfrac{ \partial C}{\partial z^{l}_{j}} \]
然后可以再推演两步:
\[ \delta^{l}_{j} = \dfrac{ \partial C}{\partial z^{l}_{j}} = \dfrac{ \partial C}{\partial a^{l}_{j}} \dfrac{ \partial a^{l}_{j}}{\partial z^{l}_{j}} = \dfrac{ \partial C}{\partial a^{l}_{j}} \sigma' (z^{l}_{j}) \]
推导
输出层的误差矩阵
由上面的单个神经元误差公式,可以得出输出层误差矩阵公式(注意这里使用大写的“L”表示输出层,圆圈表示的Hadamard乘积可以看附录):
\[ \because \delta^{L}_{j} = \dfrac{ \partial C}{\partial z^{L}_{j}} = \dfrac{ \partial C}{\partial a^{L}_{j}} \dfrac{ \partial a^{L}_{j}}{\partial z^{L}_{j}} \] \[ \therefore \delta^{L} = \dfrac{ \partial C}{\partial a^{L}} \odot \dfrac{ \partial a^{L}}{\partial z^{L}} \]
而由于我们采用的损失函数非常容易求出C对aL的导,所以公式可以进一步简化成:
\[ \delta^{L} = (a^L - y) \odot \sigma' (z^{L}) \]
某一层的误差矩阵
首先推导下单个神经元误差\(δ^l_j\)与下一层(l+1层)的关系:
\[ \begin{aligned} \delta^l_j = \dfrac{ \partial C}{\partial z^l_j} &= \sum_{k=1}^{sum(l+1)} \dfrac{ \partial C}{\partial z^{l+1}_k} \dfrac{ \partial z^{l+1}_k}{\partial z^l_j} \\ &= \sum_{k=1}^{sum(l+1)} \dfrac{ \partial C}{\partial z^{l+1}_k} \dfrac{ \partial z^{l+1}_k}{\partial a^l_j} \dfrac{ \partial a^l_j}{\partial z^l_j} \\ &= \sum_{k=1}^{sum(l+1)} \delta^{l+1}_{k} \dfrac{ \partial (w^{l+1}_{kj} a^l_j + b^{l+1}_k)}{\partial a^l_j} \sigma' (z^{l}_{j}) \\ &= \sum_{k=1}^{sum(l+1)} \delta^{l+1}_{k} w^{l+1}_{kj} \sigma' (z^{l}_{j}) \end{aligned} \]
上面推导中比较难理解的可能是累加k的由来,这是因为第\(l_{th}\)层第\(j_{th}\)个神经元会影响到第\((l+1)_{th}\)层的所有神经元,所以在反向计算偏导时需要考虑第\((l+1)_{th}\)层的所有神经元。
然后可以得出第lth层的误差矩阵(向量)\(δ^l\)的公式:
\[ \delta^{l} = ((w^{l+1})^{T} \delta^{l+1}) \odot \sigma' (z^{l}) \]
这次变换出现了矩阵转置,可能也比较难以理解其由来。仔细观察上面\(w^{kj}\)会发现其中的j与k的顺序与w的原始定义中的顺序发生了对调,这可以理解成转置的原因。自己拿一个示例演算一下也能发现从单个神经元误差到某层神经元的误差矩阵变换时的规律。
误差与权重w的关系
在得到了单个神经元的误差之后,再来看看误差与w的关系:
\[ \dfrac{ \partial C}{\partial w^l_{jk}} = \dfrac{ \partial C}{\partial z^l_{j}} \dfrac{ \partial z^l_{j}}{\partial w^l_{jk}} = \delta^{l}_{j} \dfrac{ \partial (w^l_{jk} a^{l-1}_k + b^l_j)}{\partial w^l_{jk}} = a^{l-1}_k \delta^{l}_{j} \]
和上节的推演一样,若写成矩阵,则是如下形式:
\[ \dfrac{ \partial C}{\partial w^l} = \delta^{l} (a^{l-1})^T \]
误差与偏差b的关系
与上面w的推导过程一致,容易得到误差与b的关系:
\[ \dfrac{ \partial C}{\partial b^l_j} = \delta^{l}_{j} \]
这个的矩阵形式就很简单了:
\[ \dfrac{ \partial C}{\partial b^l} = \delta^{l} \]
总结
通过上面惨无人道的推导,可以发现在经过一次正向传播之后,可以通过输出层的误差、快速求解出C对每个w和b的偏导,即∂C/∂w、∂C/∂b,再对每个w和b加上Δw、Δb,从而使得“球往下滚”,C、即Loss越来越小,神经网络在朝着我们期望的方向进行调整。
BP神经网络的训练流程
基于上面的知识,我们现在可以总结出训练一个神经网络的全流程:
- 初始化神经网络,对每个神经元的w和b赋予随机值;
- 输入训练样本集合,对于每个样本,将输入给到神经网络的输入层,进行一次正向传播得到输出层各个神经元的输出值;
- 求出输出层的误差,再通过反向传播算法,向后求出每一层(的每个神经元)的误差;
- 通过误差可以得出每个神经元的∂C/∂w、∂C/∂b,再乘上负的学习率(-η),就得到了Δw、Δb,将每个神经元的w和b更新为 w+Δw、b+Δb;
完成训练之后,一般情况下我们都能得到一个损失比较小的神经网络。
附录
矩阵
矩阵加法、减法
要求两个矩阵大小(行数、列数)相同,然后相同位置的元素相加/相减。
矩阵乘法
这个应该都还记得,即左边矩阵的一行乘上右边矩阵的一列,因此矩阵相乘要求左边矩阵的列数等于右边矩阵的行数。
\[ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix} = \begin{bmatrix} a*1 + b*2 & a*3 + b*4 \\ c*1 + d*2 & c*3 + d*4 \end{bmatrix} \]
转置
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵(即第m行第n列元素转为第n行第m列元素),用符号T表示:
\[ \begin{bmatrix} a & b & c\\ d & e & f \end{bmatrix} ^ T = \begin{bmatrix} a & d \\ b & e \\ c & f \end{bmatrix} \]
向量
只有一行的矩阵称为行向量,只有一列的矩阵称为列向量。 行向量例如:
\[ \begin{bmatrix} a & b \end{bmatrix} \]
列向量例如:
\[ \begin{bmatrix} 1 \\ 2 \end{bmatrix} \]
PS:向量只是一种特殊的矩阵,矩阵乘法和转置都是可以用在向量上的。
Hadamard乘积:⨀
假设S和T是两个同样维度的向量,使用S⨀T来表示按元素的乘积。所以 S⨀T 的元素就是\((S⨀T)_j=S_jT_j\)。
\[ \begin{bmatrix} a \\ b \end{bmatrix} \odot \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \begin{bmatrix} a*1 \\ b*2 \end{bmatrix} \]
向量的模(长度或大小)
在线性代数中,向量的大小用向量两边加双竖线表示,向量的大小就是向量各分量平方和的平方根。 如有向量S:
\[ S = \begin{bmatrix} a \\ b \end{bmatrix} \]
则其模为:
\[ \lVert S \rVert = \sqrt {a^2 + b^2} \]